online conference poster for CogSci2020

Learning sequential patterns from graphical programs

A fundamental question in cognitive science is how people infer structured, rule-like mental representations (Fodor, 1975).

We are addressing this question by introducing an experimental paradigm called “Track-A-Mole”, in which participants predict the step-wise movements of a cartoon mole on a two-dimensional space.

The movements of the mole are generated by underlying graphical programs.

Figure 1: (PDF version)

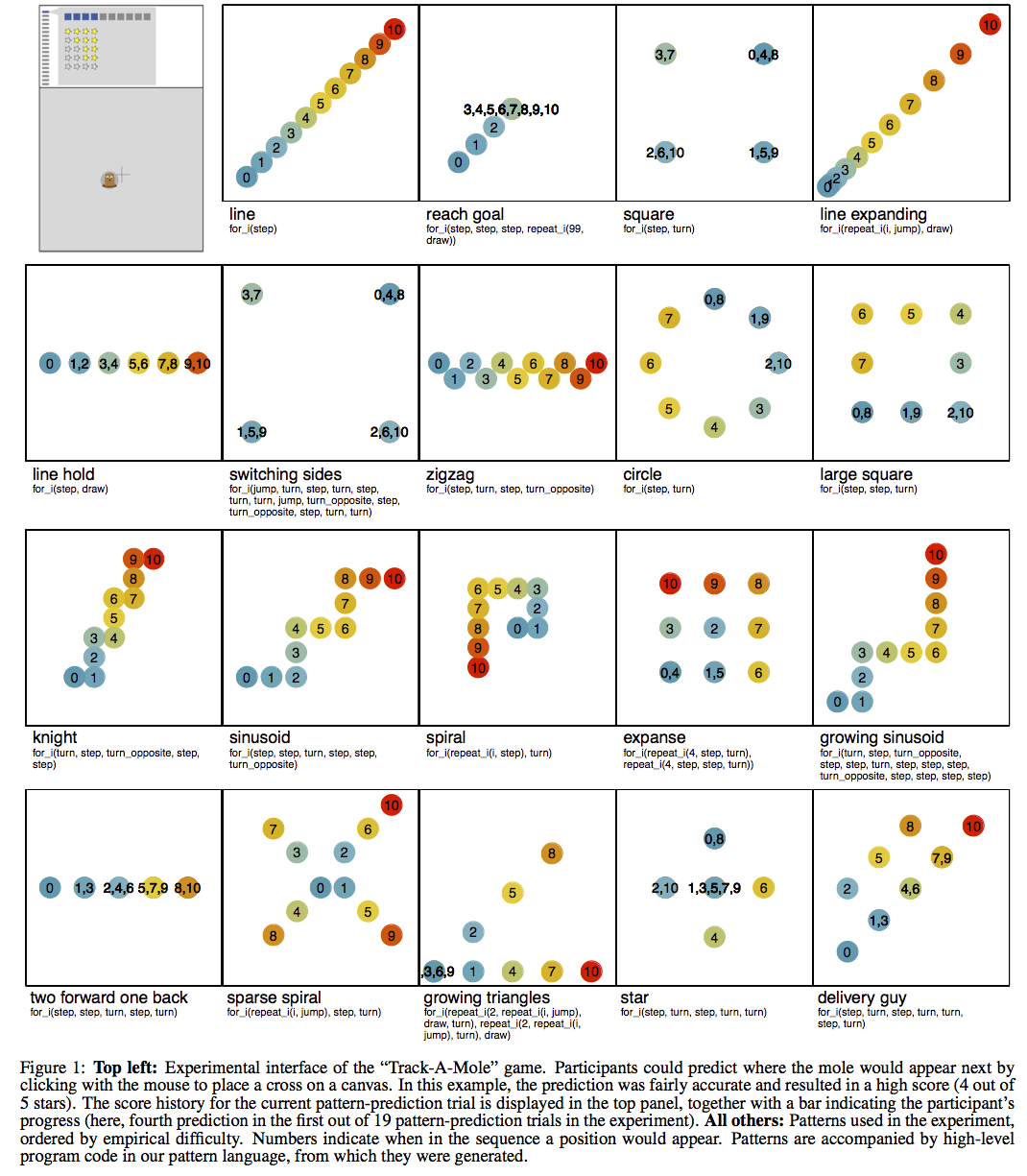
Graphical programs for sequential patterns

The programs are built from a few meaningful building blocks, such as jump, which moves the mole along its current direction and turn, which changes its current direction. All programs are wrapped in a for-loop, which executes the code inside repeatedly, for example for_i(jump, turn).

With a mixture of continuous and symbolic features (e.g., various jump sizes, angular changes of direction, countable repetitions, and loops) that are governing these patterns and that have to be inferred by people, this domain is richer than previously studied paradigms (e.g., Amalric et al., 2017).

Results

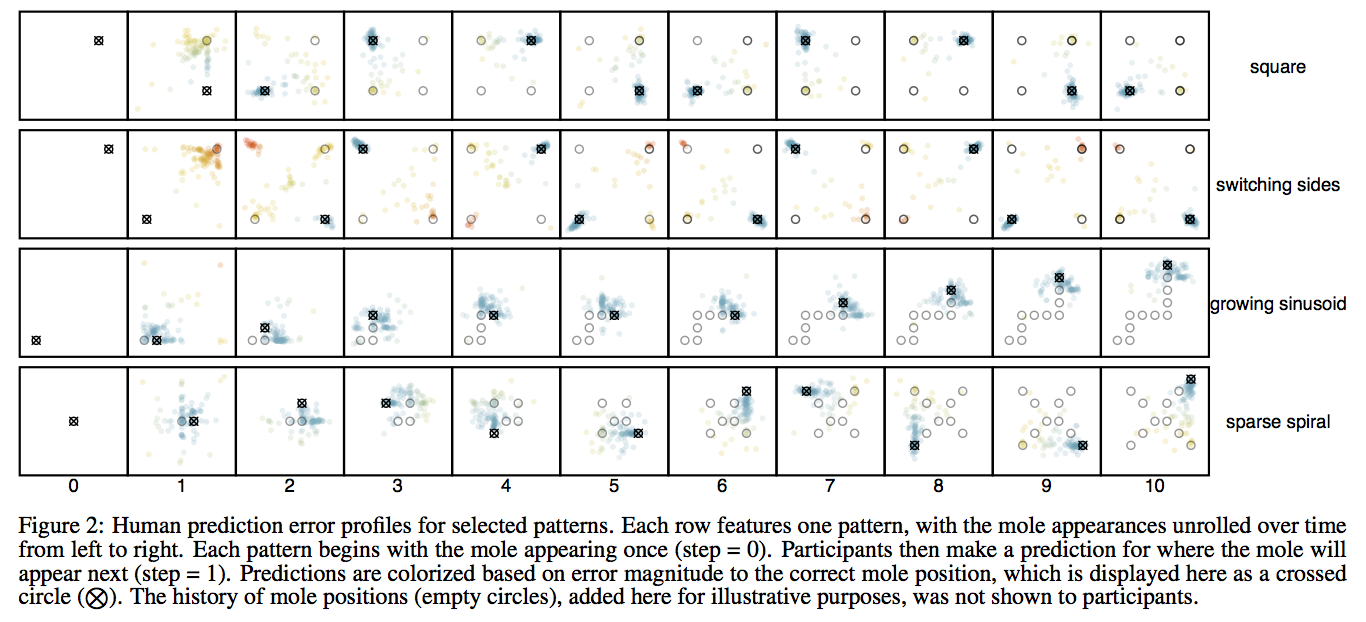
96 participants were tested on Amazon Mechanical Turk. Many people inferred the patterns quickly (i.e., after observing a few steps; e.g., see the pattern “square” in Figure 2 below).

When people made errors, they were usually not random (e.g., participants predicted the mole to appear in a corner but the wrong one; see the pattern “switching sides”).

People seemed to assume a more parsimonious pattern structure at first, which they then updated to a more complex one later on (see “growing sinusoid” and “sparse spiral”).

Figure 2: (PDF version)

Which patterns were more difficulty to learn and why?

We defined three estimates of pattern difficulty, which turned out to correlate strongly with each other (rho from .85 to .93):

• how many people learned the pattern
• the number of correct predictions averaged across people
• the point of insight (i.e., how early people identified the pattern)

They are shown below as “B: Learned”, “C: Correct predictions”, and “D: Point of insight.”

Figure 3: (PDF version)

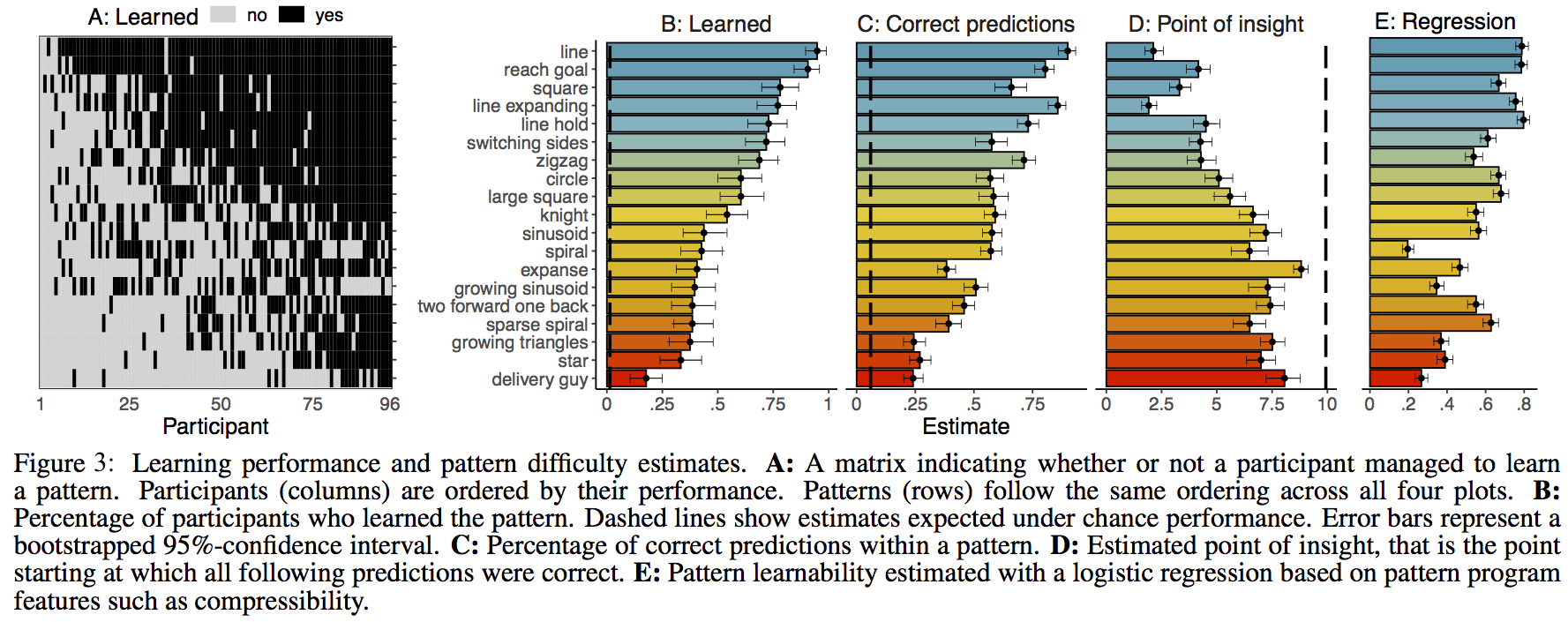
Finally, we aimed to predict pattern difficulty from the features of their specific graphical programs (e.g., how often turn occurred).

We regressed these features onto whether a participant had learned a pattern or not in a mixed-effects logistic regression, with random intercepts for participants. “E: Regression” in the figure above shows the pattern difficulty estimates generated from the regression model.

Predictive of more difficult patterns was the number of explicitly encoded terms in the program code (e.g., turn, repeat, i, jump). The repeat command allows for compressed program representations and the loop counter variable i enables the iterative growing of pattern parts such as in spirals.

Discussion

Some patterns were generally easier to learn than others, a difficulty grade that we were able to trace back to features of the programs expressing the patterns. Pattern difficulty was in part predicted by features reflecting the program complexity, such as the number of explicitly encoded movements, and the program’s compressibility, exploited by repetitions. These are typical features of programming code, but could not be identified with traditional rule- or function-learning approaches (e.g., Schulz et al., 2017).

In ongoing work, we are developing a model of the pattern learning process, based on a search through the space of possible graphical programs.

References